
二进制与数制转换
数制
数制也称为“计数制”,是用一组固定的符号和统一的规则来表示数值的方法。任何一个数制都包含两个基本要素:基数和位权。
数码
数制中表示基本数值大小的不同数字符号。例如,十进制有10个数码:0、1、2、3、4、5、6、7、8、9。
不同语言中数码
汉语

希腊文
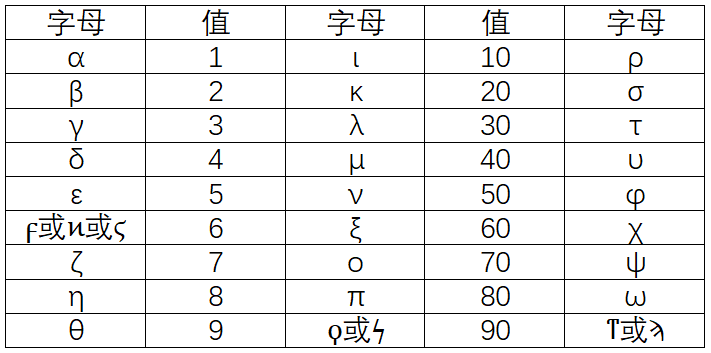
罗马文
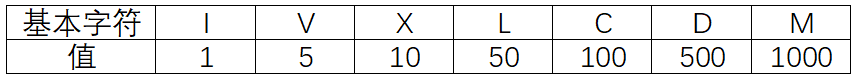
基数
数制所使用数码的个数。例如,二进制的基数为2;十进制的基数为10。
位权
数制中某一位上的1所表示数值的大小(所处位置的价值)。例如,十进制的123,1的位权是100,2的位权是10,3的位权是1。二进制中的 1011 (一般从左向右开始),第一个1的位权是8,0的位权是4,第二个1的位权是2,第三个1的位权是1
进制
进制也就是进位计数制,是人为定义的带进位的计数方法(也有不带进位的计数方法,比如原始的结绳计数法,唱票时常用的“正”字计数法)。
十进制
人类天然选择了十进制。人们在日常生活中最熟悉的进位计数制。在十进制中,数用0,1,2,3,4,5,6,7,8,9这十个符号来描述。计数规则是逢十进一。
由于人类解剖学的特点,双手共有十根手指,故在人类自发采用的进位制中,十进制是使用最为普遍的一种。成语“屈指可数”某种意义上来说描述了一个简单计数的场景,而原始人类在需要计数的时候,首先想到的就是利用天然的算筹——手指来进行计数。
二进制
在计算机系统中采用的进位计数制。在二进制中,数用0和1两个符号来描述。计数规则是逢二进一,借一当二。为区别于其它进制,二进制数的书写通常在数的右下方注上基数2,或在后面加B表示,其中B是英文二进制Binary的首字母。
八进制
由于二进制数据的基数R较小,所以二进制数据的书写和阅读不方便,为此,在小型机中引入了八进制。八进制的基数R=8=2^3,有数码0、1、2、3、4、5、6、7,并且每个数码正好对应三位二进制数,所以八进制能很好地反映二进制。八进制用下标8或数据后面加O表示 例如:二进制数据 (11 101 010 . 010 110 100)2 对应八进制数据 (352.264)8 或352.264O。
十六进制
由于二进制数在使用中位数太长,不容易记忆,所以又提出了十六进制数。
十六进制数有两个基本特点:它由十六个数码:数字0~9加上字母A-F组成(它们分别表示十进制数10~15),十六进制数运算规律是逢十六进一,即基数R=16=2^4,通常在表示时用尾部标志H或下标16以示区别,在c语言中用添加前缀0x以表示十六进制数。
数制符号
二进制 B (binary)
八进制 O (octal)
十进制 D (decimal)
十六进制 H (hexadecimal)
进制转换
十进制转二进制
十进制数除2取余法,即十进制数除2,记录下余数,得到的商值继续除2,依此步骤继续向下运算直到商为0为止。再将余数倒序即为二进制数。

二进制转十进制
把二进制数按权展开、相加即得十进制数。权:二进制数第1位(从右边数)的权值是2的0次方,第2位的权值是2的1次方……

X进制转十进制
按权展开求和,X进制数和二进制数转换为十进制数的规律是相同的。把X进制数按位权形式展开多项式和的形式,求其最后的和,就是其对应的十进制数——简称“按权求和”。





